articles/Lighting/inverse-square-page2

Inverse Square Dave Montizambert's Creating With Light - part 2 of 1 2

by Dave Montizambert Published 01/06/2014

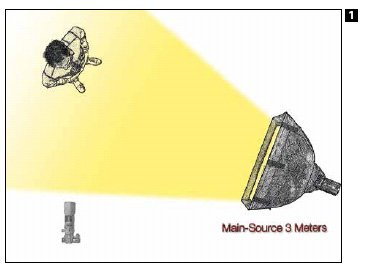
Now let's put it to use - imagine if you will, a light source pointed directly at a subject positioned 3 metres away, and let's say that the camera exposure is set to provide a correct exposure with the light at this distance. If I moved the light from 3 metres to 1 metre while keeping it directly pointed at the subject and with the power setting on the light unchanged as well as the camera exposure unchanged, what do you think a capture of this would look like compared to the first? Obviously overexposed! We all know that when you move the light close to the subject, the subject gets brighter, but why does this actually happen? The answer is energy to area - the spread of light covers a smaller distance when it is closer and so is more intense. Let's say that at 3 metres away one trillion photons of light strike the subject at any given millisecond. If the distance between the light-source and the subject is cut from 3 metres to 1 metre (see Diagrams 001 & 002) we find that while the same number of photons are being emitted from this source, they will have had less distance to spread out and so are travelling closer to one another - they are more tightly packed at the time of impact on your subject. When you think about light emitting from a point source or any given point of a broad light source, you probably imagine these photons racing out one after another in a straight line in a 'single-file' fashion. Each photon does travel in a straight line but they race out from that point in every direction over a 180˚ radius. This multi-directional emittance pattern causes the photons to spread out from one another more and more as they get further away from their source, so when the light source is far from your subject the photons will have more distance to spread out and conversely when the light is close to your subject the photons will have less distance to spread out. At 1 metre the photons are covering 1⁄9th of the area that they were covering at 3 metres and so 9 times as many photons will strike the subject. So if 1 trillion photons are striking our subject when the light is 3 m away, how many photons would strike it when it's only 1 m away? Take the change in distance, multiply it by itself, then invert - 1⁄3 x 1⁄3 = 1⁄9 which becomes 9 times more photons, the answer is: 9 x 1 trillion = 9 trillion photons at the 1 metre distance.

You are probably thinking, that's all great from a theoretical standpoint but knowing how many photons are striking doesn't tell me how to interpret the final figure as an f-stop, or a shutter speed, or an ISO setting, or a power setting so that I can get back to a correct exposure. To do this you need know that a 1 stop hike increases exposure by 2 times and that a 1 stop drop decreases exposure by 1⁄2. To correct for the 9 times increase in brightness using what we just learned, we must think; image is currently 9 times over exposed so cut the exposure to 1⁄9th. How many stops is 1⁄9th? If one stop decrease in exposure is 1⁄2, then 2 stops must be 1⁄4, and 3 stops must be 1⁄8th and so on (keep half-ing the last fraction). For a perfect exposure, 1⁄9th requires a 3.125 stop adjustment,1⁄8th is as close as one can get on a DSLR to 1⁄9th since its apertures, shutter speeds, and ISO can only be set in 1⁄3rd or 1⁄2 stop increments, besides it isn't really worth worrying about since 0.125 of a stop is pretty much negligible. If your light-source has continuous fade control then you could dial in the exact exposure and leave the camera settings as they are.

Knowing the Inverse Square Law really speeds up the photographic process for me, it let's me think things through without going to the trouble of physically doing them to see how it might or might not work out. For example it helps me with shooting decisions on the fly such as: if I double the distance of the background from subject the background will have to become physically 4 times bigger to cover the same area in my camera frame, or how about, if I move the light four times further away I know that the exposure will have to increase by 4 stops, can my light give me that much more power to cover that or do I need to come up with another solution. The Inverse Square Law diminishes 'shoot-stress' and frustration freeing my brain to concentrate more on my subjects and other creative aspects of the shoot. The technical mathematical side of photography and lighting needs to be intuitive, it has to become second nature through practise and contemplation, otherwise it is a hindrance rather than a boon to creating great, imaginative images.

Bio

Dave Montizambert lectures internationally on lighting, digital photography, and Adobe Photoshop. He is also a published author having written two books on lighting and digital photography (www.montizambert.com ) plus numerous magazine articles on these topics in North America, Europe, Russia and Asia. Dave also creates Lighting and Photoshop tutorial DVDs for www.software-cinema.com and www.photoshopcafe.com. Dave is available for lectures and workshops in your area and can be reached through www.montizambert.com.

Please Note:
There is more than one page for this Article.
You are currently on page 2

• Inverse Square Dave Montizambert's Creating With Light page 1
  
• Inverse Square Dave Montizambert's Creating With Light page 2
  

Contact Dave Montizambert

1st Published 01/06/2014
last update 09/12/2022 14:55:16

More Lighting Articles

There are 23 days to get ready for The Society of Photographers Convention and Trade Show at The Novotel London West, Hammersmith ...
which starts on Wednesday 15th January 2025